Um eine Vorstellung der Heugabel-Bifurkation zu
erhalten, geht man genauso, wie bei den vorangegangenen Bifurkationen vor,
zuerst betrachten wir ein dynamisches System:
die Differentialgleichung vom nichtlinearen Typ wird
wieder eine Stufe komplizierter gewählt, das ist der Typ von
Differentialgleichung (in Normalform), bei dem Heugabel-Bifurkationen
auftreten:
.
Auch hier werden die stationären Lösungen der
Differentialgleichung und Aussagen über deren Stabilitätsverhalten gesucht.
Die
stationäre Lösung ist gegeben durch:
Û 
Û 
Dynamische Variable und Kontrollparameter sind
reell, für m < 0 würde der Wurzelausdruck aber komplexe
Werte annehmen, was zu einem Widerspruch führt. Demzufolge existieren für m < 0 die Fixpunkte 
nicht!
Warum die Punkte 
zusammengefaßt betrachtet werden, ergibt sich im Verlauf der
folgenden Rechnung.
Für die drei Fixpunkte ist die lineare
Stabilitätsuntersuchung durchzuführen. Zuerst muß die Differentialgleichung
für kleine Auslenkungen 
linearisiert werden.
Im
allgemeinen Fall lautet die linearisierte Differentialgleichung:
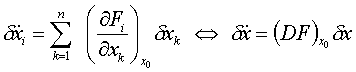
Für
den vorliegenden Fall ergibt sich also:
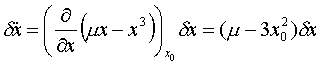
und somit für die Determinante der Jakobi-Matrix der
Ausdruck 
, das Problem ist eindimensional.
Anschaulich lassen sich die Stabilitätsüberlegungen
für die Fixpunkte wieder mit den anschwellenden und abklingenden
Exponentialfunktionen durchführen:
Betrachten wir nun den 1. Fixpunkt und die
zugehörige linearisierte Differentialgleichung:
.
Die allgemeine Lösung dieser linearisierten
Differentialgleichung lautet:
.
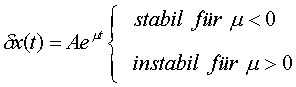Für den 2. und 3. Fixpunkt und die zugehörige,
linearisierte Differentialgleichung ergeben sich:
.
Für
beide Fixpunkte gilt also dieselbe Gleichung.
Die allgemeine Lösung dieser linearisierten
Differentialgleichung lautet:
stabil, da m > 0
.
Der Fixpunkt 
ist also stabil für m > 0 (stabiler Knoten) und instabil für m < 0 (Sattelpunkt), die Fixpunkte 
sind stabil, da m > 0 (stabiler Knoten), für m < 0 existieren die Fixpunkte 
nicht.
Im Parameterraum ergibt sich damit folgendes Bild:
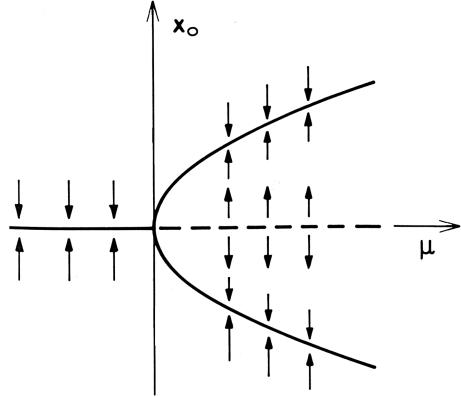
Ein Fixpunkt ändert seine Stabilität unter Entstehung zweier neuer Äste. Das Bild im Parameterraum inspiriert den Namen Heugabel- oder Stimmgabel-Bifurkation (engl. pitchfork bifurcation).