3.4 Hopf-Bifurkation

 

Die Hopf-Bifurkation unterscheidet sich von den vorangegangen Bifurkationstypen. Die wesentlichen Bedingungen für das Auftreten einer Hopf-Bifurkation sind:

das dynamische System hat mindestens zwei Komponenten die Jacobi-Matrix hat zwei konjugiert komplexe Eigenwerte statt des Wechsels von einem Fixpunkt zu einem anderen geht ein Fixpunkt in einen Grenzzyklus über.

 

Die Hopf-Bifurkation ist keine Eigenwert-Null-Bifurkation!

 

Es handelt sich also um einen komplizierteren Bifurkationstyp. Dementsprechend läßt sich eine anschauliche Vorstellung nicht ganz so simpel aufbauen. Ein einfaches Beispiel ist das Differentialgleichungssystem:

 

               I

               II           .

 

Um erste Aussagen treffen zu können, bietet sich eine Transformation auf Polarkoordinaten an, mit:

 

,

 

sowie bilden der Linearkombinationen

 

I× + II×    und    -I× +  II×

 

ergeben sich die entkoppelten Differentialgleichungen:

 

                                      und                  .

 

Die Differentialgleichung für r hat die gleiche Form, wie die Differentialgleichung der Heugabel-Birfurkation, es können also die Lösungen mit r0 übernommen werden.

Die zeitliche Änderung des Winkels ist konstant, hier kann es keine stationären Lösungen geben, also auch keine Bifurkation.

Der 1. Fixpunkt ergab sich bei der Heugabel Bifurkation zu:

 

                             Ù               

 

mit der linearisierten Differentialgleichung:

 

  .

 

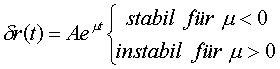Für den 2. und 3. Fixpunkt ergaben sich:

 

                             Ù      

 

mit der linearisierten Differentialgleichung:

 

                               stabil, da m > 0

 

Trägt man wiederum die Fixpunkte über dem Kontrollparameter auf, so ergibt sich folgendes Bild:

 

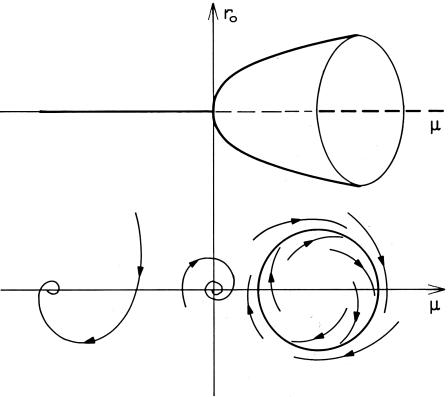
- siehe Mathematica-Notebook -

 

Die Betrachtung der entkoppelten Differentialgleichungen erklärt nur anschaulich, warum für die dynamische Variable r bei Variation des Kontrollparameters m eine Bifurkation auftritt.

Zieht man ferner in Betracht, daß das Problem mehrdimensional ist, läßt sich erklären, warum aus dem zweidimensionalen Bild der Heugabel Bifurkation der dreidimensionale Paraboloid im obigen Diagramm wird.

 

Um präzise Aussagen über das Verhalten des dynamischen Systems bei Variation von m treffen zu können, muß die Lineare Stabilitätsanalyse durchgeführt werden. Die Rechnung und Ergebnisse sind im beiliegenden Mathematica-Notebook aufgeführt.

 

Demnach beschreibt  die zweite Lösung stabile Kreisbahnen, in die sich alle Bahnen sowohl von außen als auch von innen spiralförmig mit konstanter Winkelgeschwindigkeit  hineinwenden. Die Bezeichnung ist im allgemeinen "Grenzzyklus" (engl. limit cycle).

 

In etwas anderer Darstellung:

 

 

 

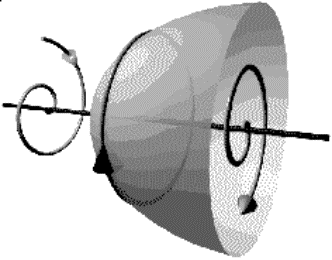
Hopf-Bifurkation: benannt nach dem Mathematiker E. Hopf.