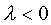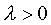Die Sattel-Knoten-Bifurkation gehört zusammen mit
der transkritischen und der Heugabel-Bifurkation zu der Gruppe der
"Eigenwert-Null-Bifurkationen". Charakteristisch für diese Bifurkationen ist
ein verändertes Stabilitätsverhalten des Fixpunktes bei Vorzeichenwechsel des
zugehörigen Eigenwertes der Jakobi-Matrix, also:
|
Eigenwert-Null-Bifurkationen:
|
Um ein anschauliches Verständnis der Sattel-Knoten-Bifurkation
zu erhalten, betrachten wir ein dynamisches System:
wobei der Übersichtlichkeit halber das System
eindimensional sein soll. Als Differentialgleichung verwenden wir den einfachsten
nichtlinearen Typ, das ist der Typ von Differentialgleichung (in
Normalform), bei dem Sattel-Knoten-Bifurkationen auftreten:
.
Wie anfangs schon erläutert, sind bei einem
physikalischen System dynamische Variable und Kontrollparameter reell.
Gesucht sind nun die stationären Lösungen der
Differentialgleichung, um Aussagen über deren Stabilitätsverhalten treffen zu
können.
Die
stationäre Lösung ist gegeben durch:
Û 
Û 
Ein erstes wichtiges Ergebnis kann hier schon
abgelesen werden: Dynamische Variable und Kontrollparameter sind reell, für m < 0 würde der Wurzelausdruck
aber komplexe Werte annehmen, was zu einem Widerspruch führt. Demzufolge
existiert für m < 0 kein Fixpunkt!
Nun folgt die lineare Stabilitätsuntersuchung.
Zuerst muß die Differentialgleichung für kleine Auslenkungen 
linearisiert werden.
Im
allgemeinen Fall lautet die linearisierte Differentialgleichung:
.
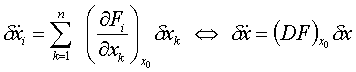Für
den vorliegenden Fall ergibt sich also:
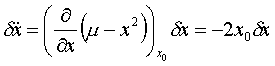
und
somit für die Determinante der Jakobi-Matrix der Ausdruck -2x,
das
Problem ist eindimensional.
Die
allgemeine Lösung dieser linearisierten Differentialgleichung ist:
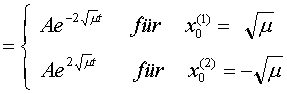
Die Begriffe Sattelpunkt und stabiler Knoten sind im
Mehrdimensionalen sinnvoll (siehe gegebenenfalls "2. Lineare
Stabilitätsanalyse"), wo noch mindestens 1 weiterer, stets negativer Eigenwert existiert.
Das betrachtete System ist aber eindimensional, am
anschaulichsten sind Aussagen durch Betrachten der Lösungen der linearisierten
Differentialgleichung zu erhalten:
Für den Fall 
ergibt sich als
Lösung der linearisierten Differentialgleichung eine abklingende
Exponentialfunktion. Diese Schar von Fixpunkten ist also stabil (allgemein:
stabile Knoten).
Für den Fall
ergibt sich
als Lösung der
linearisierten
Differentialgleichung eine anschwellende
Exponentialfunktion. Diese Schar von Fixpunkten ist also instabil (allgemein:
Sattelpunkte).
Die so erhaltenen Ergebnisse stimmen mit der
Klassifizierung der Fixpunkte mittels Linearer Stabilitätsanalyse überein.
Trägt man die Fixpunkte 
über dem
Kontrollparameter m auf, so ergibt sich
folgendes Bild im Parameterraum:
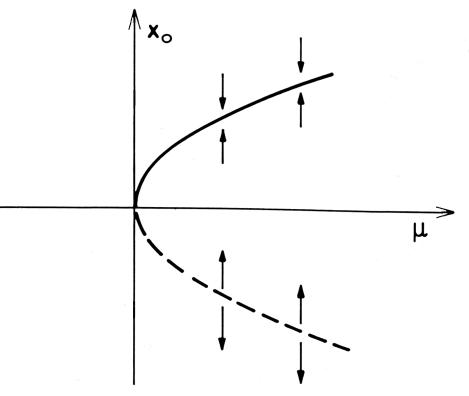
Ein Sattelpunkt und ein stabiler Knoten vereinigen
sich und verschwinden dann, denn für m < 0 existiert kein Fixpunkt. Am
Bifurkationspunkt 
entsteht ein
sogenannter Sattel-Knoten.
Daher der Name: Sattel-Knoten-Bifurkation !